學習原因：

已經有寫程式的基本能力，需要開始對程式的效能有點概念。雖然說先求有，再求好，但也得知道什麼是好。不要求每次都寫出最佳解，但至少要學會判斷哪個比較好。這篇內容將介紹什麼是演算法和如何判斷程式碼的效能好壞。

學習目標：

• 了解什麼是演算法
• 了解如何使用 Big O Notation 並比較不同演算法的效能。

演算法 Algorithm

是告訴計算機在特定的步驟和邏輯下如何處理數據。目標是 經過一系列精確的操作，將輸入轉換成所需的輸出。

可以比喻為烹飪食物的食譜，就像食譜告訴你在特定的順序和方式下如何處理食材，然而這個處理步驟對於不同人可以有不同的處理方法。

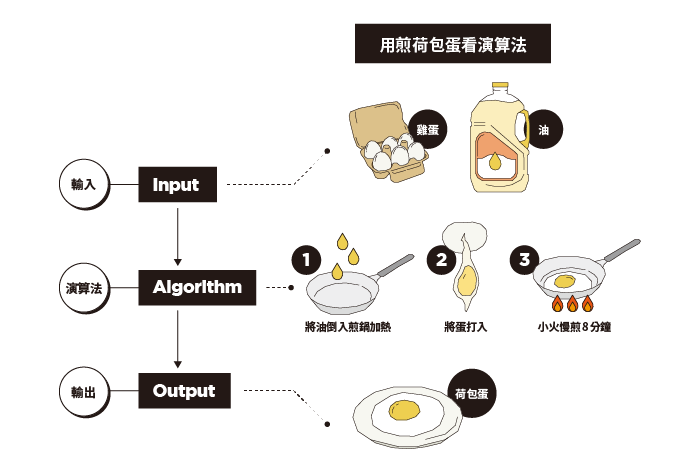
圖片來源：https://www.eisland.com.tw/Main.php?stat=a_yg2Y8Hs

處理同一件事情，演算法可以有很多種寫法，但 好的演算法 通常具有以下特點：

• 正確性：確實地解決問題，並產生正確的結果。
• 效率：在合理的時間內完成，避免不必要的資源浪費。
• 清晰性：步驟應該清晰易懂，方便理解和實現。
• 通用性：能夠應用於不同的情況，而不僅僅限於特定案例。

參看以下例子，在 已排序又不重複的 數列中找出目標資料的位置，分別用 2 種演算法處理：

• Linear Search 線性搜索：

  使用 For Loop 取出每個數值，再與目標值作比對，找到就回傳位置並跳出 function.

  def linear_search(numbers, target):
  
  	for i, num in enumerate(numbers):
  		# 若找到目標的數值則回傳數值的 index
  		if num == target:
  			return i
  
  		# 找不到資料則回 -1
  		return -1
  
  print(linear_search([1, 2, 5, 6, 7], 1)) # should print 0 
  print(linear_search([1, 2, 5, 6, 7], 6)) # should print 3
  

• Binary Search 二分搜索：

  • 把數列對半切開，使用中間值 mid 與目標值 target 作比對

  

  圖片來源：https://learncodingfast.com/binary-search-in-python/

  • 若大於 mid 時，更新右邊的位置為 mid + 1。
  • 若小於 mid 就，更新右邊的位置為 mid - 1。
  • 否則就是等於目標值，就可以回傳出去了
  • 若沒有回傳，就繼續重複以上的動作，直到找到為止。

def binary_search_position(numbers, target): 
    left = 0
    right = len(numbers) - 1 
    while left <= right:
        mid = (left + right) // 2   
        if numbers[mid] > target:
            right = mid - 1
        elif numbers[mid] < target:
            left = mid + 1
        else:
            return mid              
        
    return -1

print(binary_search_position([1, 2, 5, 6, 7], 1)) # should print 0 
print(binary_search_position([1, 2, 5, 6, 7], 6)) # should print 3

以上 2 種不同的演算法，都能找出目標值的位置，但怎樣判斷哪個演算法的效能比較好？先來學習 Big O Notation 的概念吧。

Big O Notation

是用於 描述函式漸近行為 的漸進符號，屬於數學符號的一種。
它用作描述一個函式數量級的 漸近上界。

我們會用作判斷演算法的效能指標，分別會有 2 個維度：

• 時間複雜性 Time Complexity
  • 愈多的輸入，在最壞的情況下，對 運行次數 的影響
• 空間複雜性 Space Complexity
  • 愈多的輸入，在最壞的情況下，對 空間使用 的影響

不過，現在一般都只會討論 Time Complexity，因為隨著計算機硬體的發展讓我們可以處理更大的記憶體容量，許多應用程序可以在較大的記憶體中運行，並且很少受到空間使用的限制。這減少了對空間效率的關注。

另外，需要注意 Big O Notation 只是一個粗略估算，若要更精確地評估演算法的性能，可能需要考慮常數因素、實際執行環境、硬體特性等。

來看看例子怎樣使用 Big O Notation

def print_int(n):
   print(n)

不管 n 是多大，也只會執行一次，所以 Time Complexity 標記為 O(1)

def sum(n):
   total = 0
   for i in range(n):
       total += i
   return total

在最壞的情況，for loop 就是要執行 n 次，n 愈大，運行次數會是 n 次，所以標記為 O(n)

def multiple(n):
   for i in range(n):
       for j in range(n):
           print(i * j)

在最壞的情況，第一個 for loop 執行 n 次，第 2 個 for loop 要執行 n * n 次，所以標記為 O(n^2)

經過簡單的例子，應該有點概念怎樣標記 Big O Notation，然後運行次數愈多，就是代表效能較差，所以基本上看 Big O 的數值就能比較它們的效能，再參考以上這個圖，更好判斷效能怎樣是比較好

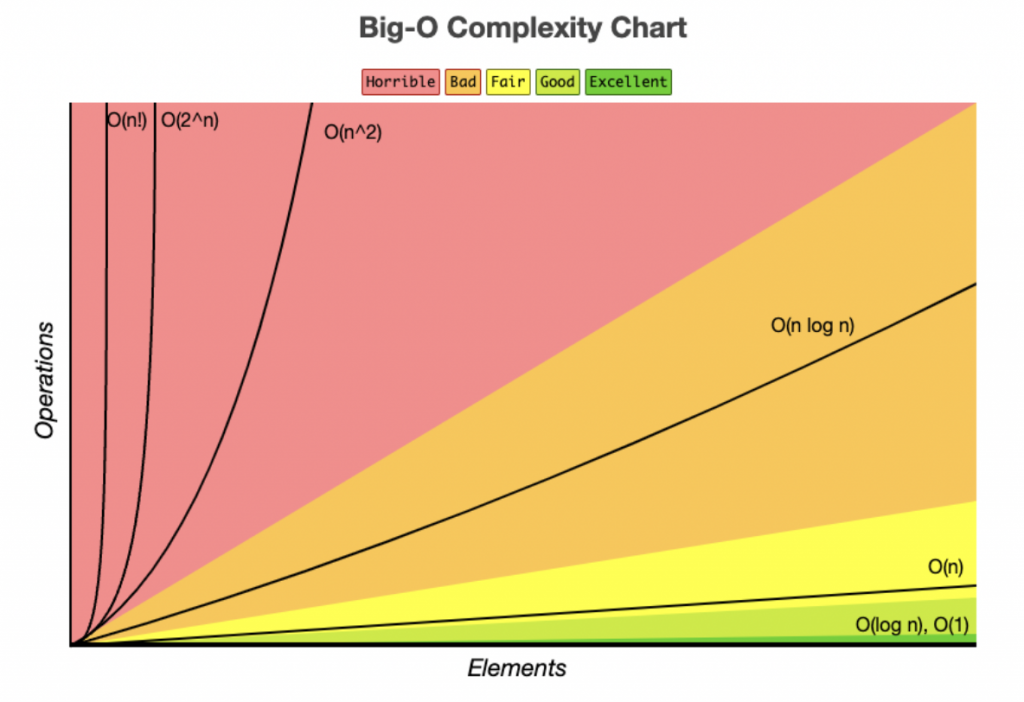
圖片來源： https://www.freecodecamp.org/news/big-o-cheat-sheet-time-complexity-chart/

我們實作的時候蠻容易會寫出雙層迴圈，其實這個已經是 O(n^2) 了，效能是偏差。所以日後當你能力足夠的時候，開始要想想怎樣重寫可以提高效能。

好了，再回來看看 Linear Search 和 Binary Search 的比較

def linear_search(numbers, target):
	for i, num in enumerate(numbers):
		if num == target:
			return i
	return -1

不管 numbers 有多少個，最壞就是執行 n 次，所以是 O(n)

而 Binary Search：
當你只有 2 個數值，在最壞的情況，需要執行 1 次，就找到位置
當你只有 4 個數值，在最壞的情況，需要執行 2 次，就找到位置
當你只有 8 個數值，在最壞的情況，需要執行 3 次，就找到位置
當你只有 16 個數值，在最壞的情況，需要執行 4 次，就找到位置

可以看到規律是 2x = n，透過 對數 的換算 x = log n，故會標記 Time Complexity 為 O(log n)

根據 Big O Complexity Chart，很清楚知道 Binary Search 的效能比 Linear Search 好。

不過 Binary Search 的應用有限制，需要是已排序的才能應用，而 Linear Search 則沒有這限制。所以還是得看情況選用，除了這 2 種搜尋方式，其實還有其他演算法，不妨去發掘一下。

到這裡有一點的程式能力，也學會怎麼判斷演算法的效能，其實可以挑戰一下刷 Leetcode 的 Easy Level 了，寫不出最佳解也沒關係，先嘗試解出來，再 Google 或是用 ChatGPT 參考別人的解法。